马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?立即注册

x
临床能量需求的估算 " ~7 a0 x1 {6 q/ T* _
: ~6 p! s, {4 Q% s# I' t) e- I7 @/ k& |1 m
) V! a" w/ F2 q4 l I* z1 |
正文5 ^8 F" S+ H6 O4 r; R! r; i% i
9 t' D5 a7 ^0 J$ g1 s P0 F
能量消耗有多种,如静息能量消耗(resting energy expenditure,REE)、基础能量消耗(basal energy expenditure,BEE)、 每日静息能量消耗(resting daily energy expenditure,RDEE)、每日总能量消耗(total daily energy expenditure,TDEE)等。准确预测人体能量需求是实施营养健康咨询及临床营养支持的先决条件,能量需求的预测方法有两类 :①测定法(measurement),即测定每日能量消耗(measured daily energy expenditure,MDEE),具体方法有量热计(calorimeter)直接测热法、代谢车间接测热法(metabolic cart indirect calorimetry); ②估算法(estimation),即估算每日能量消耗(estimated daily energy expenditure,EDEE),具体方法是用公式计算。直接测热法既昂贵又复杂、只能在实验研究中使用 ;间接测热法基层单位难以普及。估算法虽然没有测定法精确,但是简易、方便、价廉。目前业已发表的估算公式共有 200 多种,分别估算不同条件下的能量消耗及需求[1] 。本文介绍几种常用的估算法,并分析不同公式的优缺点及其适用人群。+ l5 Q& S9 B4 |- E2 ?: M' D* |0 A
( f2 ~7 r( g$ ]2 G; b H

3 o: q* H# c; J* |: i( z3 y+ l7 g9 [0 h3 Z4 W
1 Harris-Benedict 方程式
0 J; h: E$ N& l1 F
3 J `% F+ G7 L9 e9 C1 H! |/ @' ?Harris-Benedict 方程式(Harris-Benedict equation,HBE)可能是人类历史上第一个 REE 预测公式[2] ,测定法及其它估算法均在其后。HBE 始建于 1919 年,是在 239 例健康成年人(男女分别为 136、103 例)的数据基础上形成的,包括年龄、性别、身高及体重 4 个基本变量。在计算 TDEE 时还要考虑活动、发热、创伤及营养不良等附加因素。原始 HBE 如表 1。$ Q. |# H8 _5 p, w& {
4 j# {0 B& p3 K$ U" w, G
$ f& m9 H w! y$ g, |4 u9 @- w
* O Q) h& ~& N. A+ G9 r研究发现 HBE 偏向(适用)于营养良好的青年人及非肥胖人群,其估算值比间接测热法测定值高 6%~15%。Garrel DR 等[3]报告一组 67 例健康志愿者,HBE 计算值比测定静息代谢率(resting metabolic rate,RMR)平均高 21%,其高估值大小与 RMR 高低呈负相关,即 RMR 越高,其高估值越小(越接近实际情况),RMR 越低,其高估值越大。所以, HBE 对 RMR 较低的女性及瘦体组织(lean body mas,LBM)减少的患者有很大的高估风险。由于 HBE 个体差异较大,该公式对体重丢失、急慢性疾病、营养不良患者的价值有限[3, 4] 。对于肿瘤患者,Alpers D 等[5]人建议在 HBE 计算值的基础上乘以 1.3,用以估算肿瘤患者的 TDEE。但是,Bauer J 等[6]报告,HBE 乘以 1.3 后其估算值显著高于间接测热法测定值。
5 I! I# m6 t5 I+ Y0 j& t6 w3 F6 i2 Cunningham 公式. C1 Y' o5 j6 K+ C/ I) [) a8 A% H
4 V4 b# U" N) W/ Q1980 年 Cunningham JJ [7] 利用 Harris JA 及 Benedict FG 的 239 例受试者的原始数据,排除 16 例运动员的数据后,回归分析发现 LBM 是基础代谢率(basal metabolic rate,BMR)的唯一显著有效预测因素,年龄、性别、身高及体重均是 LBM 的影响因素,与 BMR 无明显直接关系。因此,得出基于 LBM 的公式如表 2。) _. n& [% I; u* s
& `" _/ U" S- L- h! j1 P1 s5 z1 O0 M* z7 D1 e4 z* r; q7 r
) ~9 P7 U' A. ]7 `6 D' o6 Z, l公式中的LBM计算方法是Moore FD等人[8] 1963年建立的,具体见表 3。% ]2 J, M. T, W+ G9 g5 X+ j/ w/ R4 C
' K1 u+ | X9 k$ q7 ^
* q6 g, t0 ]: n
V- c% @! R3 o) z+ [6 z2014 年 ten Haaf T 及 Weijs PJ 报 告[9] ,Cunningham 公式能够准确预测运动员(recreational athlete)的能量需求,而 HBE、FAO/WHO/UNU、Mifflin 及 Owen 公式对该人群的预测准确性均低于 50%。, L8 z. i9 x; f2 x2 m" Z2 p' F; N' ]
( r2 f- @5 @( }( {) X) L3 Shizgal-Rosa 方程式; ]7 k, |4 C |# f) @; [
: a% H3 U$ p2 M鉴于 HBE 的缺陷,1984 年 Roza AM 及 Shizgal HM [10] 用 Harris JA 及 Benedict FG 当年的原始数据结合新的数据,对原始 HBE 进行了重新评价与修订,改良后的 HBE 如表 4,又称为 Shizgal-Rosa 公式。研究发现,该公式与实际能量消耗更加接近,更加准确。在 1990 年 The Mifflin-St Jeor 公式出现之前,Shizgal-Rosa 方程式是最为准确的 REE 预估公式。
1 y) t g% m4 ]& M5 y& w. t
, w8 k: M1 G$ e7 A7 J# L+ `6 H, J: f) x$ _
/ h3 u' u+ Z0 ^& C' j% o7 k
在对体重、身高、年龄、性别及体细胞群(bodycell mass,BCM)进行综合分析后,Roza AM 及 Shizgal HM 发现,传统 HBE 的年龄、性别、身高及体重 4 个变量实际上都与 BCM 密切相关,或者说可以由 BCM 替代,所以,他们又提出了基于 BCM 的另外一个 REE 计算公式,如表 5。 A( A5 r. Y9 w0 R% B; i- C- ~2 _
1 r+ O& }) x) s$ ^
" J9 Y# N( M& P! C& C
9 N2 X/ [0 y. L. \Owen 方程式
* K4 }: b# g( c' R& @7 {
% H b/ J' F! I0 [1986 年 Owen OE 等[11]用间接测热法测量了 44 例 18~65 岁,体重 43~143 kg 健康女性的能量消耗,其中有 8 位运动员。多因素回归分析发现,只有体重与 RMR 关系最为密切,而且运动员与非运动员有显著差别。由此,他们建立了 Owen 方程式,见表 6。
# N( g" I2 V$ w; r6 h0 [ I R$ X4 T
* l; [3 P! B: Q/ U, l% I2 w4 v- A* N( e; R4 r4 x: Z0 O# \6 Q% L8 D
3 L, [6 c; u4 q# I2 w0 e$ AHasson RE 等[12]对 362 名 18~60 岁成年人的研究发现,Owen 方程式比较适用于 50~60 岁年龄组的人群。Siervo M 等人[13]对 157 例青年白人妇女的研究发现,Owen 公式适用于指导体重正常青年女性的营养咨询。- Z& ]/ y* Z0 n0 J% J: Q
* m0 g- Z, v% A% {8 Y5 Mifflin-St Jeor 公式1 ]7 ]# d7 ~( K+ b/ b
, p5 y& R9 T. ^5 c4 ]8 ?
1990 年 Mifflin MD 等[14] 人提出了一个更好的 REE 计算公式,如表 7。' Y0 ?) `6 Y* V' P1 ^% X& M
: L: k2 u6 W( G8 L5 x1 Q) r
$ D# ~& r8 F# _7 d! {& U/ [ L. o$ `2 p# t% U6 c' L/ ^
在系统分析的基础上,2005 年美国营养师学会(The American Dietetic Association,ADA) 认为 Mifflin-St Jeor 公式是目前计算 REE 的最佳方法[15] ,2008 年美国临床营养学会(American Society for Clinical Nutrition,ASCN)官方杂志 —《美国临床营养杂志》有同样的推荐报告[16] 。Mifflin-St Jeor 公式对普通成年人 REE 的评估误差率在 10% 以内,但是该公式对老年人及不同种族人群有一定的差异,该公式不适用于只有肌肉而没有脂肪的举重运动员。$ ?, l7 g2 ^$ w
S% s& F6 Q% G8 i
6 WHO/FAO/UNU 公式
, h" o3 _% X/ ?* l6 L
% k; u; T3 b8 B' {1985 年 WHO/FAO/UNU 提出了他们基于体重以及基于体重及身高的两个 BMR 计算公式[17] ,表 8。
$ |( l# x: c) z) R4 W, t% k! K/ o( `* V; @# e$ D
: ~! {: ?8 q: ]: L( G
" n: z# P: c8 Q( [( p, ?WHO/FAO/UNU 公式的数据主要来源于年轻的欧洲军人及警察,男性 2279,女性 247。尽管年龄在 19~82 岁之间,但是,实际上老年人很少。研究报告 WHO/FAO/UNU 公式对老年人的 RMR 预测不够精确,低估与高估并存,而且不适合肥胖人群[15] 。
! Z' q2 a6 ]0 d& N5 E
) }4 F1 j M$ @) f3 }" ~$ {TDEE 是指一天(24 小时)的总能量消耗,包括休息时的能量消耗及活动时的能量消耗两个部分,其中前者占 2/3(REE 相当于 TDEE 的 60%~80%),后者占 1/3。WHO/FAO/UNU 根据个体活动情况将 TDEE 分为 6 类 :①非常不活动但并非卧床者,TDEE=REE× 1.2 ;②不活动(很少或没有运动,办公室工作)者,TDEE=BMR×1.2 ;③轻度活动(每周 1~3 天轻度活动 / 运动)者,TDEE=BMR×1.375 ;④中度活动(每周 3~5 天中度活动 / 运动)者,TDEE=BMR× 1.55 ;⑤重度活动(每周 6~7 天重度活动 / 运动)者,TDEE=BMR×1.725 ;⑥超重活动(极重的活动 / 运动,重体力劳动或每天 2 次训练如马拉松、竞赛等)者,TDEE= BMR×1.9 。7 I( W# M2 e! {9 j8 Z
* c7 _0 Y7 J: \+ K& i, I7 拇指法则(rule-of-thumb,ROT)1 A9 {9 s! D7 n0 P% n5 L3 b
2 f$ K5 H0 n K' ?& ^+ [
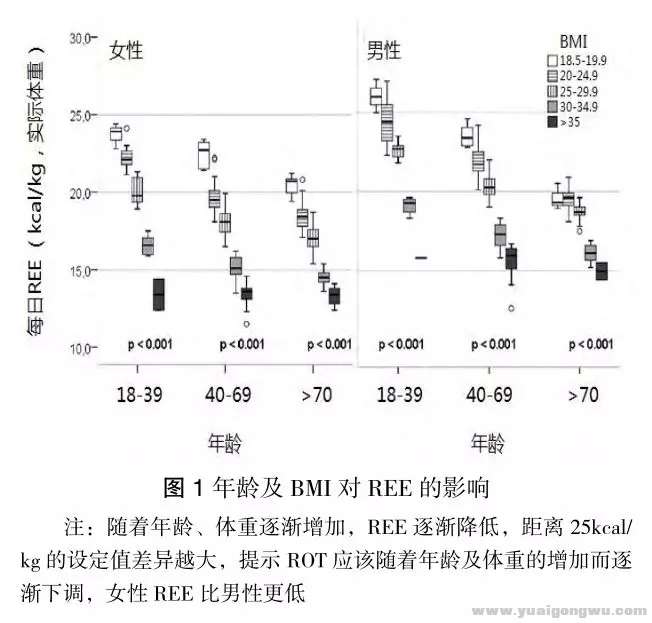
经典的拇指法则是每日能量需求为 25kcal/kg,传统上,25kcal/kg 的计算值是活动患者的 REE 或不活动患者的 TDEE,其中的体重为理想体重。由于每日能量需求受年龄、性别、BMI、运动及应激等因素的影响,所以 ROT 值不应该是一个恒定数值,而应该动态调整。随着体重增加,ROT 值应该下调,因为增加的体重是脂肪组织,而脂肪组织是非活跃器官。Zauner A 等[18]建议对体重正常、超重、肥胖、病态(严重)肥胖患者分别使用 25kcal/kg、22kcal/kg、20kcal/kg、16kcal/kg 计算其 REE。同样,随着年龄的增加,成年后每 10 年 REE 下降 1%~2%,ROT 也应该下调,因为肌肉逐渐减少,而脂肪组织的比例相对升高。Valentini L等[19]对 5 家医院 676 例连续入院患者用 HBE 计算其 REE,发现即使采用理想体重计算,ROT 的 25kcal/kg 也高估了 95% 患者的能量需求,而且随着年龄增加、随着体重增加,其高估值越大,而且还有显著的性别差异,图 1。有鉴于此,ESPEN 2009 指南推荐 25kcal/kg 是患者的 TDEE,而不是 REE,只有在极少数严重应激状态下,才需要 30kcal/kg [20] 。Valentini L 等[19]还建议,创伤、疾病等应激条件下计算 TDEE 时,根据年龄、性别及体重调整后的 REE 应该乘以应激系数,但是主张降低传统的应激系数数值,将系数根据应激轻、中、重分为 1.1、1.2 及 1.3 三个等级,见表 9。
# ?& c# ^; w- ~1 d6 e$ Z7 ?
* s. _) Q7 P; _( O
 $ c K5 v; ^6 a7 q: G% i% F
$ c K5 v; ^6 a7 q: G% i% F

S7 T( C, T% I+ u9 i2 o; {
8 ^, O) s% X6 I9 ^. W8 人体成分估算法" V7 _1 u+ l5 k1 `3 p* k
/ d/ c4 M; w/ }/ e. r! U* C根据代谢率不同,人体组成可以分为8个部分,即脑、心、肝、肾、骨骼肌、骨骼、脂肪组织及其他组织,其能量需求(消耗)各不相同,骨骼为 2.3kcal/(kg∙d),骨骼肌为 14.5kcal/(kg∙d),脂肪组织为 13kcal/(kg∙d),肾脏、心脏为 440kcal/(kg∙d),脑 240kcal/(kg∙d),肝脏 200kcal/(kg∙d)。脑、肝、心、肾尽管占全部体重不足 6%,但是其总能量消耗占 REE 的 60%~70%,骨骼肌尽管占全部体重的 40%~50%,但是其能量消耗只占 REE 的 20%~30% [21, 22] 。不同器官组织的耗能比例见图 2。
: k/ f5 Q$ _4 e# I8 N9 I
; G- R$ b: X$ ?, c3 v4 c: ], d6 p9 g- H7 W3 U
8 x" ]3 ]- }1 |, N! p
根据不同组织、器官的代谢率,Elia M [23] 提出了一个 REE 计算(Calculation of REE,REEc) 公式,见表 10。' ?7 p% ]2 a6 t$ [5 L" e# a; h
/ W' Q+ O2 ^4 P) @5 c8 F
: ~' [+ z R! X5 r l9 T& @: t t/ i
人体成分估算法没有实际操作价值,但是它对理解肿瘤条件下的能量消耗有重要意义。脑、肝、心、肾为高代谢器官,其重量的微小变化可以导致能量消耗的显著变化,脑、肝、肾的原发肿瘤或继发肿瘤增加了所在器官的重量,使得所在器官能量消耗显著增加,机体处于高代谢状态,能量负债加大,进而导致营养不良及恶液质。
7 |; C! w) h: U3 w! i( j/ a' }9 Z* e* d8 [/ s
9 小结
+ s3 G- g7 k& y+ d) G$ s; q" A
& e7 q) C! { n: Z能量需求的准确预测是临床营养支持的前提。测定法虽然相对精准,但是其操作复杂、价格不菲、要求患者空腹休息等待时间长,而且中国幅员辽阔,差异巨大,医院条件及患者病情不同,所以能量估算法有巨大的应用空间。而且,随着手机及 iPad 广泛使用,估算法将变得更加便利。尽管每一种估算法各有优缺点,研究结果参差不齐,但是 Mifflin-St Jeor 公式得到 ADA、ASCN 的一致推荐。) L( S* h& A& Z0 B
" R3 b- Q9 O/ s9 g. d2 l8 N
鉴于体重差异巨大,在实际应用过程中,应该对体重进行校正。对体重在正常范围内的人群,实际体重与理想体重基本一致,可以选择实际体重估算能量需求 ;对肥胖人群,选择实际体重会高估能量需求,选择理想体重会低估能量需求 ;Glynn CC 等[24]推荐选取实际体重及理想体重的平均值进行估算。需要指出的是,上述所有估算法均是基于正常人群的数据,疾病情况下特别是肿瘤条件下的能量消耗与需求的估算仍然有待研究。7 R# \3 Q9 m1 A
% F7 q/ ]# b/ N5 g9 c2 G3 E参考文献:(略) |